报告内容
卷积计算单元的上板测试
卷积计算电路的测试电路主要包括由ARM、输入输出 FIFO、DMA 电路以及卷积加速电路。具体流程为ARM 端发送开始指令给卷积加速器,加速器从 DDR 中读取数据 ,利用FIFO 输入数据和权重,经卷积计算电路后将数据再写入 FIFO 中,并写回 DDR 中,写回后同时反馈给 ARM , ARM 端再读取数据,通过串口打印出计算后的数据,测试电路的结果图如下:
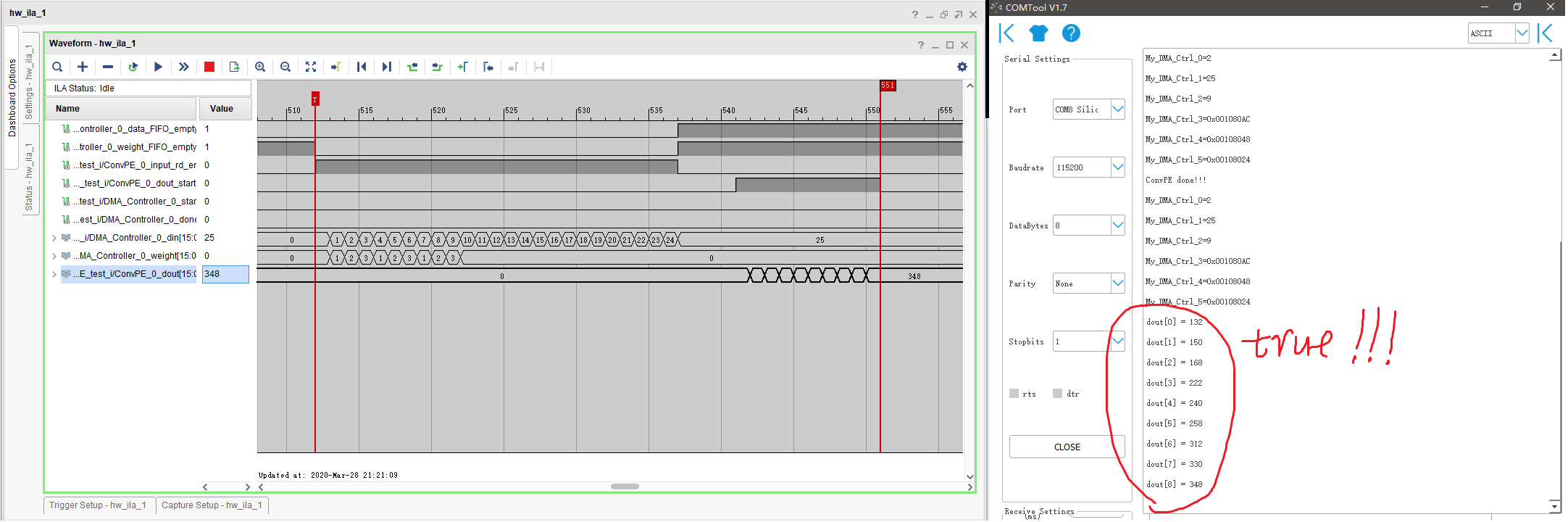
池化电路的设计与仿真
池化电路的设计与之前的卷积电路架构类似,也是利用移位寄存器进行滑窗操作,不同的是池化区域的大小为 2x2,且无权重参数,因此不需要乘法矩阵和加法树。本项目中的卷积神经网络采用的是最大值池化,因此只要将原先乘法器的位置换成最大值比较器即可,该池化电路设计原理图如下:
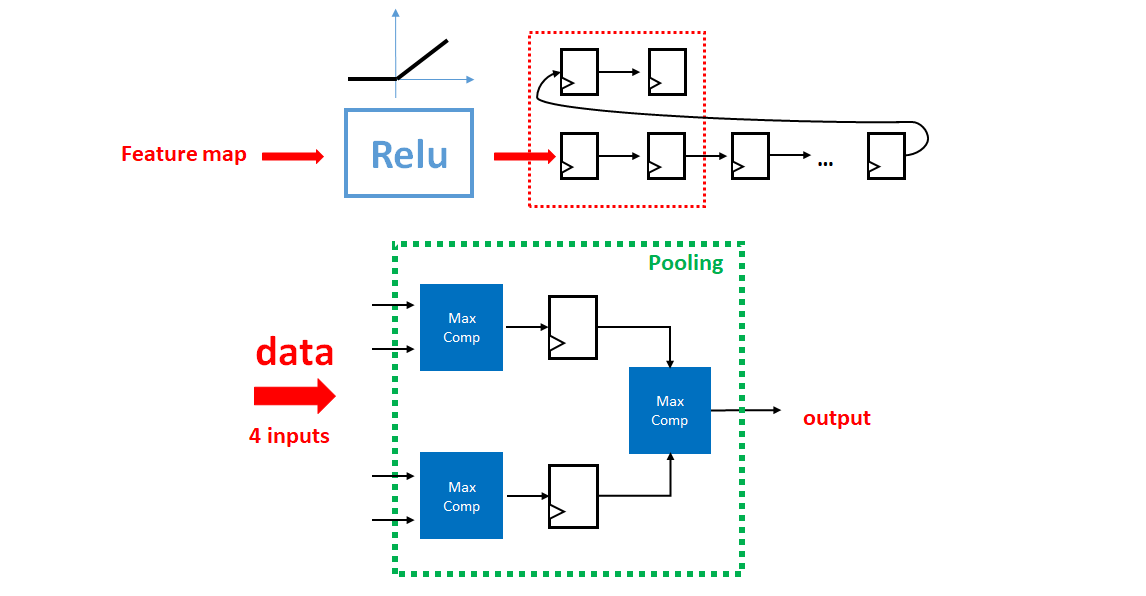
由于在池化操作中,一般常采用步长为 2 的滑窗池化,所以相比于之前卷积计算中的步长为1,需要在原来的数据剔除电路中进行改进,将其进行一般化,即考虑步长,卷积核大小,输入特征图尺寸因素,得到一个通用的数据剔除电路。具体分析如下:
为了尽可能减少数据剔除中 FIFO 缓存的等待时间,假设输入图像大小为 ${n}\times{n}$, 卷积核的大小为 ${m}\times{m}$, 步长为 $u$, 读入 $k$ 个数据后自动读出,则正确的输出数据个数为
$$
l = (\frac{n-m}{u}+1)^2\tag{1}
$$
又 FIFO 读入速度为
$$
v1 = \frac{\frac{n-m}{u}+1}{un}\tag{2}
$$
FIFO 读出速度为
$$
v2 = 1\tag{3}
$$
故为了保证数据不丢失,则
$$
\frac{k}{v2-v1} = \frac{l}{v2}\tag{4}
$$
因此
$$
k = (1-\frac{n-m+u}{u^2n})({\frac{n-m}{u}+1})^2(向上取整)\tag{5}
$$
其中 $k$ 值在 FIFO ip 核的 prog full 阈值中设定。根据 prog full 信号,读入 $k$ 个数据后自动读出。这样既保证数据的不丢失,又可以减少缓存带来的等待时间。
卷积层电路的设计
本项目中的网络模型结构有5层(除去输入输出层),包括卷积层1,池化层1,卷积层2,池化层2,全连接层。加速卷积层计算是加速该网络的核心,在卷积运算中,我们经常要对数据进行读写操作,因此需要对数据进行复用,根据卷积运算的并行方式,即有如下三种数据复用的方式:
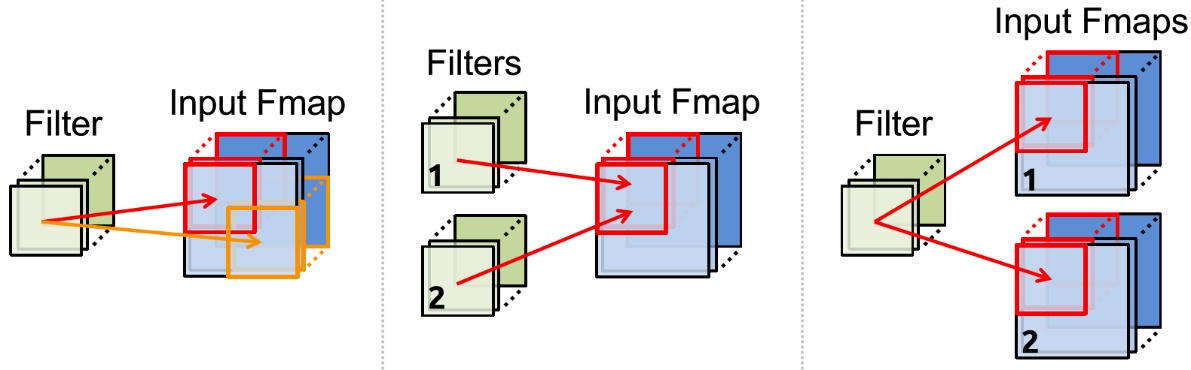
考虑到使用的FPGA开发版资源有限(DSP Slice数量为80),我设计了一个并行度为8的卷积层电路,即可同时进行8个卷积计算,我将其称之为卷积核列表(ConvPE List)。卷积核列表中包括8个卷积计算单元,每个计算单元需要9个乘法器,一共使用了72个DSP Slice,仅卷积层DSP利用率达90%。
同时,为了提高实现并行计算的效果,我将数据位宽统一为128(16x8)位。其中16是单个数据的位宽,8是卷积计算单元的个数。根据卷积神经网络的结构,卷积层含有两层,因此需要采用卷积核列表重复利用的方式,即一个电路供两次卷积层计算使用。通过上述分析,我设计了卷积层硬件电路,如图4所示:
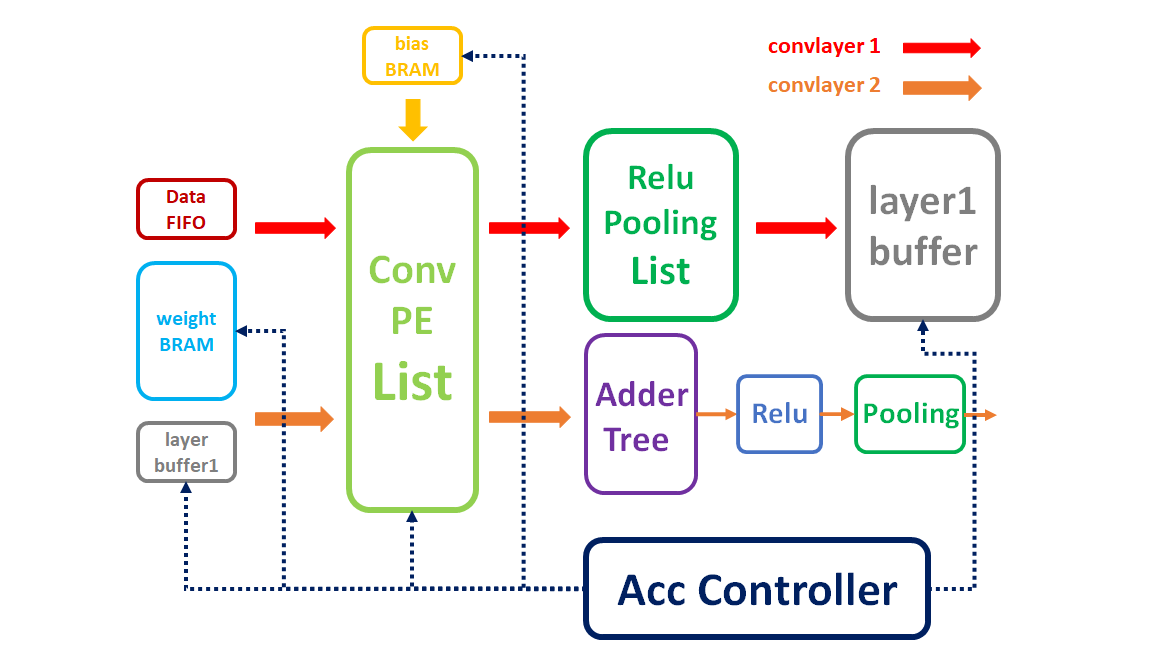
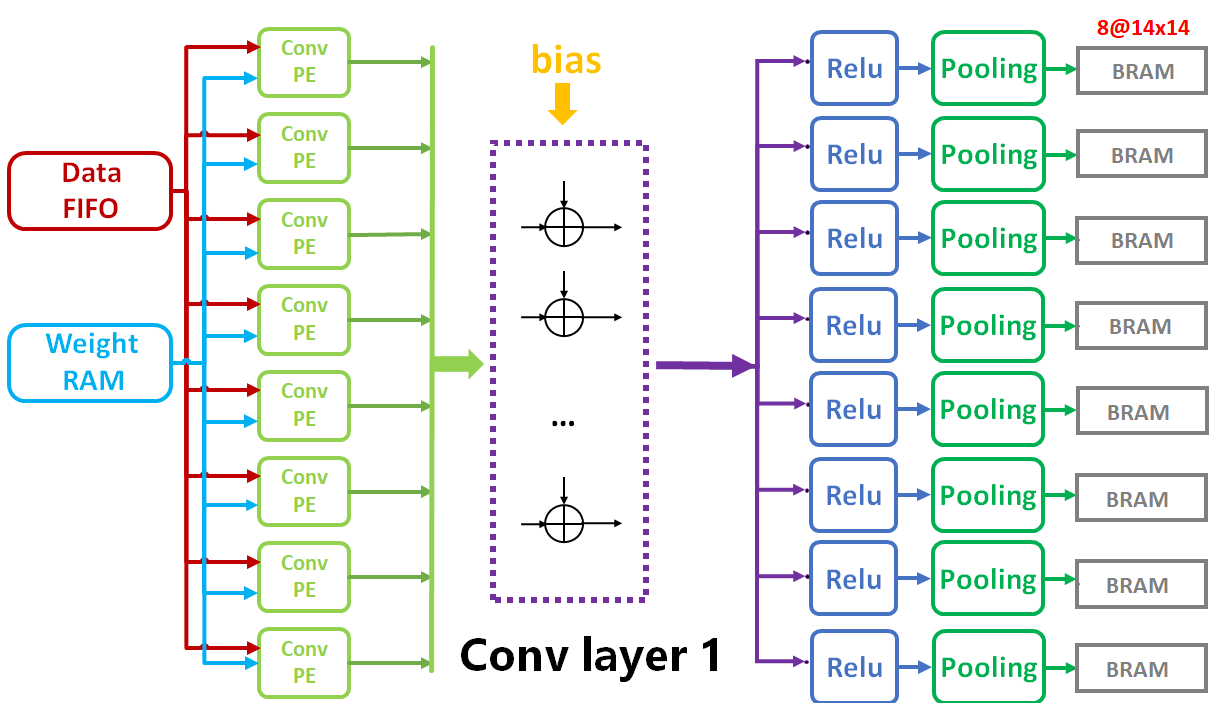
根据网络结构,第一层为单通道特征图像输入,卷积核个数为8,则一次卷积核列表计算就可以完成卷积层1 的计算,之后再经过8个 Relu 和池化电路,得到8个通道的图像输出。同时,为了尽可能地减少在数据的读取加载中消耗太多时间,我将卷积层1的输出结果存放在了FPGA的片上RAM中(Block RAM),以方便后续计算层快速读取数据,具体硬件电路架构图如下:
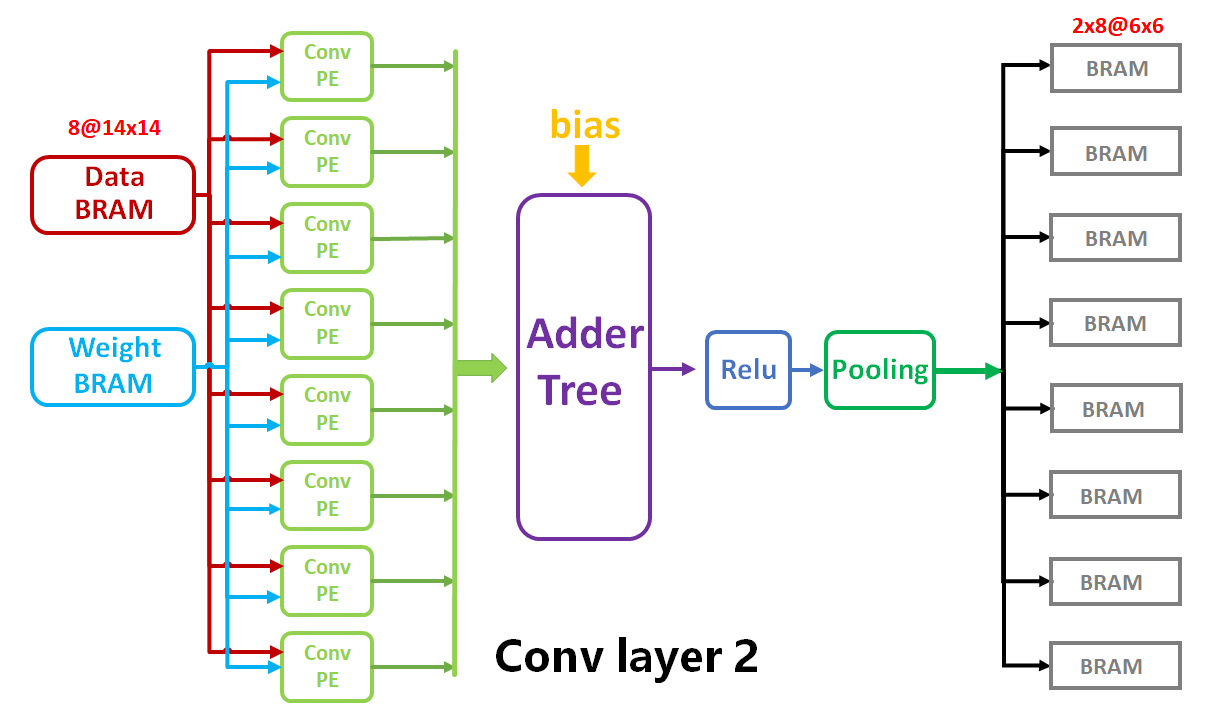
对于第二层网络,由于此时输入特征图像的通道数为8,卷积核个数为16,因为开发板的DSP资源有限,因此完成卷积层2的计算需要调用16次的卷积核列表,加法树,Relu和池化电路。数据的输入由之前存放在BRAM的图像缓存和权值缓存构成。具体的硬件电路架构图如下:
卷积层电路的结果验证
卷积层电路的验证与调试过程中,主要利用 Tensorflow 训练好的参数进行验证,打印输出各层的结果,并转换为16位的定点数进行比较。电路调试通过在仿真波形图中观察各个控制信号、输入输出数据的长度、数据同步性等。其最终仿真结果的波形图如下:
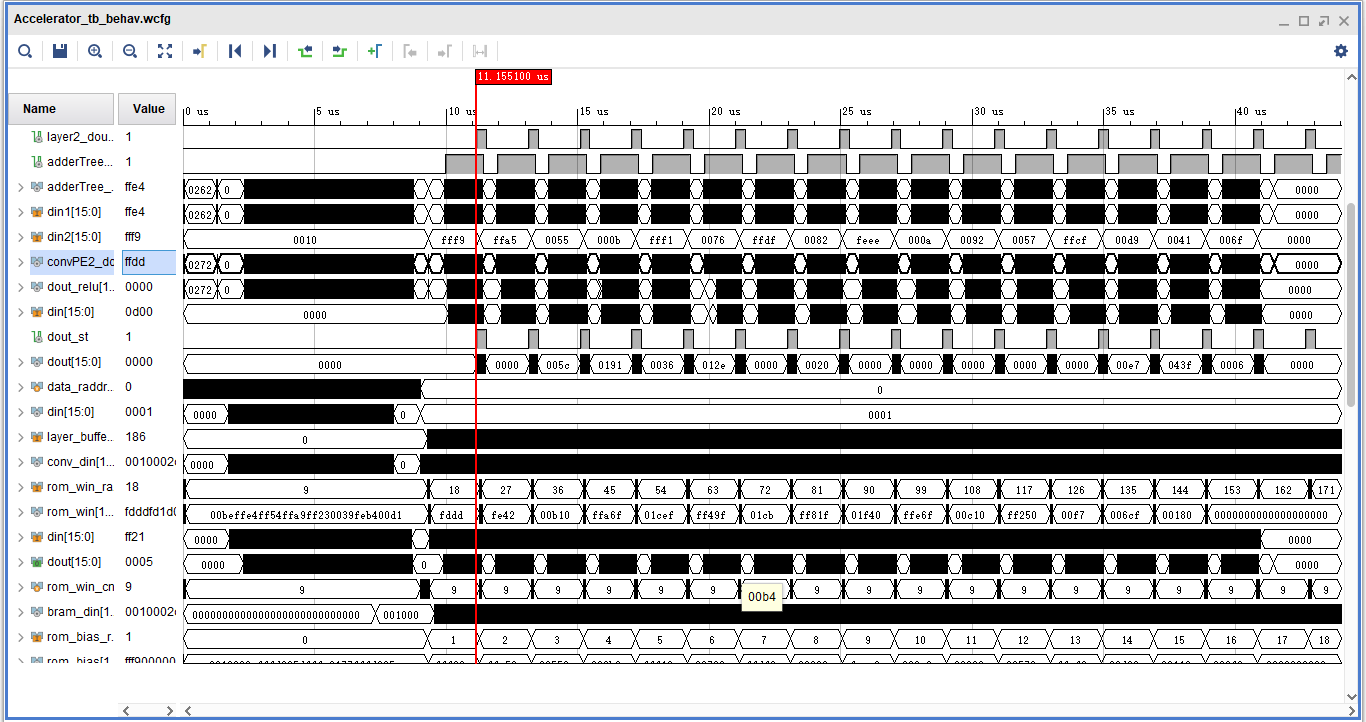
将上述卷积加速器的计算结果与 Tensorflow 输出的结果进行对比,以其中一个输出通道为例(大小为 6x6),对比结果如下:
- FPGA卷积加速器计算结果:
$$
\left[\begin{matrix}
0.0000 & 0.0000 & 0.1548 & 0.0000 & 1.4199 & 1.6777\\0.2222 & 1.2314 & 0.6880 & 0.5923 & 2.1265 & 1.4238\\1.2700 & 1.7573 & 0.0000 & 2.1201 & 2.2896 & 0.4580\\1.6187 & 1.3481 & 1.9756 & 3.1812 & 2.0439 & 0.4443\\1.2183 & 0.8091 & 0.7070 & 1.6250 & 0.9170 & 0.0137\\0.0024 & 0.0615 & 0.6807 & 1.8628 & 0.3379 & 0.0000
\end{matrix}\right]
$$
- Tensorflow计算结果:
$$
\left[\begin{matrix}
0.0000 & 0.0000 & 0.1562 & 0.0000 & 1.4209 & 1.6794\\0.2204 & 1.2317 & 0.6900 & 0.5948 & 2.1252 & 1.4247\\1.2713 & 1.7572 & 0.0000 & 2.1179 & 2.2903 & 0.0122\\1.6156 & 1.3483 & 1.9769 & 3.1808 & 2.0455 & 0.0000\\1.2183 & 0.8096 & 0.7073 & 1.6252 & 0.9191 & 0.0143\\0.0035 & 0.0623 & 0.7224 & 1.8634 & 0.3399 & 0.0000
\end{matrix}\right]
$$
- 两者误差结果:
$$
\left[\begin{matrix}
0.0000 & 0.0000 & -0.0015 & 0.0000 & -0.0010 & -0.0017\\ 0.0018 & -0.0003 & -0.0020 & -0.0026 & 0.0013 & -0.0009\\-0.0013 & 0.0001 & 0.0000 & 0.0022 & -0.0008 & 0.4458\\ 0.0031 & -0.0002 & -0.0013 & 0.0003 & -0.0016 & 0.4443\\-0.0000 & -0.0005 & -0.0002 & -0.0002 & -0.0021 & -0.0007\\-0.0010 & -0.0008 & -0.0417 & -0.0006 & -0.0020 & 0.0000
\end{matrix}\right]
$$
由上述结果可知,该卷积层电路计算基本正确,考虑到卷积神经网络具有一定的鲁棒性,因此在误差不大的情况下,对最终的识别准确率影响不会很大。
总结和计划
本月主要完成了加速器外围测试电路的搭建,数据剔除电路的通用化设计,卷积层电路的设计与仿真验证工作,对之前的电路进行了完善和改进,使卷积加速器更加通用化,以便可以适应各种不同的卷积计算,具有更广泛的应用前景。之后计划根据搭建好的测试平台,完成整个卷积加速器的上板测试,并与电脑 CPU 计算进行对比,若加速效果达到预期,则开始着手毕业论文的撰写,并进一步完善卷积神经网络加速器。