Project Review-1 本科毕业设计

报告内容

• 卷积神经网络模型的搭建和训练
• 模型的参数获取及数据的定点化
• 基于 ZYNQ 的卷积神经网络加速器架构的设计
• 卷积核计算电路的设计、仿真以及计算结果对比
• 总结和计划

CNN 模型的搭建

一种用于手写数字识别的卷积神经网络（Convolution Neural Network , 简称CNN ），参考了LeNet-5 模型，我对该模型的卷积核大小以及数量进行了调整，以便更好适配之后设计的硬件加速器，且两者的识别准确率相差不大。该网络模型包括输入层、卷积层、池化层、全连接层以及输出层。模型结构如图1所示：

其中输入图像像素大小为30x30 ,经过两组卷积层和池化层，最后连接两层全连接层。卷积层采用大小为3x3 的卷积核，步长为1；池化层采用的是2x2 区域的最大值池化；激活函数使用 ReLu 。使用 Tensorflow进行网络模型搭建，部分代码如下。在 Colab 上已经完成了模型的训练，该模型在10000 张验证集图片中准确率为98.13% 。部分源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 搭建网络结构
class MNIST_CNN(Model):
    def __init__(self):
        super().__init__()
        self.conv1 = layers.Conv2D(
            filters=8,
            kernel_size=[3, 3],
            activation=tf.nn.relu,
            padding='valid',
            name='conv2d_1',
            input_shape=(30, 30, 1)
        )
        self.pool1 = layers.MaxPool2D(pool_size=[2, 2], strides=2, name='max_pooling2d_1')
        self.conv2 = layers.Conv2D(
            filters=16,
            kernel_size=[3, 3],
            padding='valid',
            name='conv2d_2',
            activation=tf.nn.relu
        )
        self.pool2 = layers.MaxPool2D(pool_size=[2, 2], strides=2, name='max_pooling2d_2')
        self.flatten = layers.Reshape(target_shape=(6 * 6 * 16,))
        self.dense1 = layers.Dense(units=10)
        # self.dense2 = layers.Dense(units=10)

    def call(self, inputs):
        x = self.conv1(inputs)            # [batch_size, 28, 28, 8]
        x = self.pool1(x)                 # [batch_size, 14, 14, 8]
        x = self.conv2(x)                 # [batch_size, 12, 12, 16]
        x = self.pool2(x)                 # [batch_size, 6, 6, 16]
        x = self.flatten(x)               # [batch_size, 6 * 6 * 16]
        x = self.dense1(x)                # [batch_size, 10]
        output = tf.nn.softmax(x)

        return output
    
model = MNIST_CNN()

1
2
3

# 验证准确率
pred = 'Loss: {:.4f}, Accuracy: {:.4f}'
print(pred.format(test_loss.result(),test_accuracy.result()))

模型的参数获取与数据的定点化

利用 Tensorflow 的 checkpoint 函数可以对训练好的参数文件进行保存，由于在云端训练时采用的是32位的浮点数计算，故保存下来的参数是浮点数格式。但在 FPGA 上进行浮点数计算时，会消耗大量的硬件资源，可能无法在板上有限的硬件资源下完成加速器的硬件电路实现，因此需要将 浮点数做定点化处理，本次项目中使用的16位的定点数，包括1位符号位，4位整数位以及11位小数位，利用 python编写了数值转换的脚本，其部分结果如下表所示：

上述结果显示将浮点数转成定点数后，误差在$10^{-5}\sim10^{-4}$范围内，因此采用将浮点数转化为定点数表示的方法是可行的。定点数的计算对FPGA硬件资源十分友好，且16位的定点数相比32位的浮点数可以大大减少了存储资源的占用和数据的加载速度。

基于ZYNQ 的卷积神经网络加速器架构的设计

实现 CNN 加速器的整体实现流程主要通过 PC 端将手写数字图片发送至 ZYNQ 平台(包括 ARM(PL) 和 FPGA(PL) 即 ARM 接受图片数据并存放在 DDR 中，通过 AXI-GP 接口发送指令给 FPGA ，FPGA 接受到开始指令从 DDR 中读取图片数据和权值偏置参数，并完成卷积神经网络的计算，计算完成后反馈回 ARM ，最后再由 ARM 将计算结果发送回 PC 端并显示识别结果。其整体架构图如图2所示：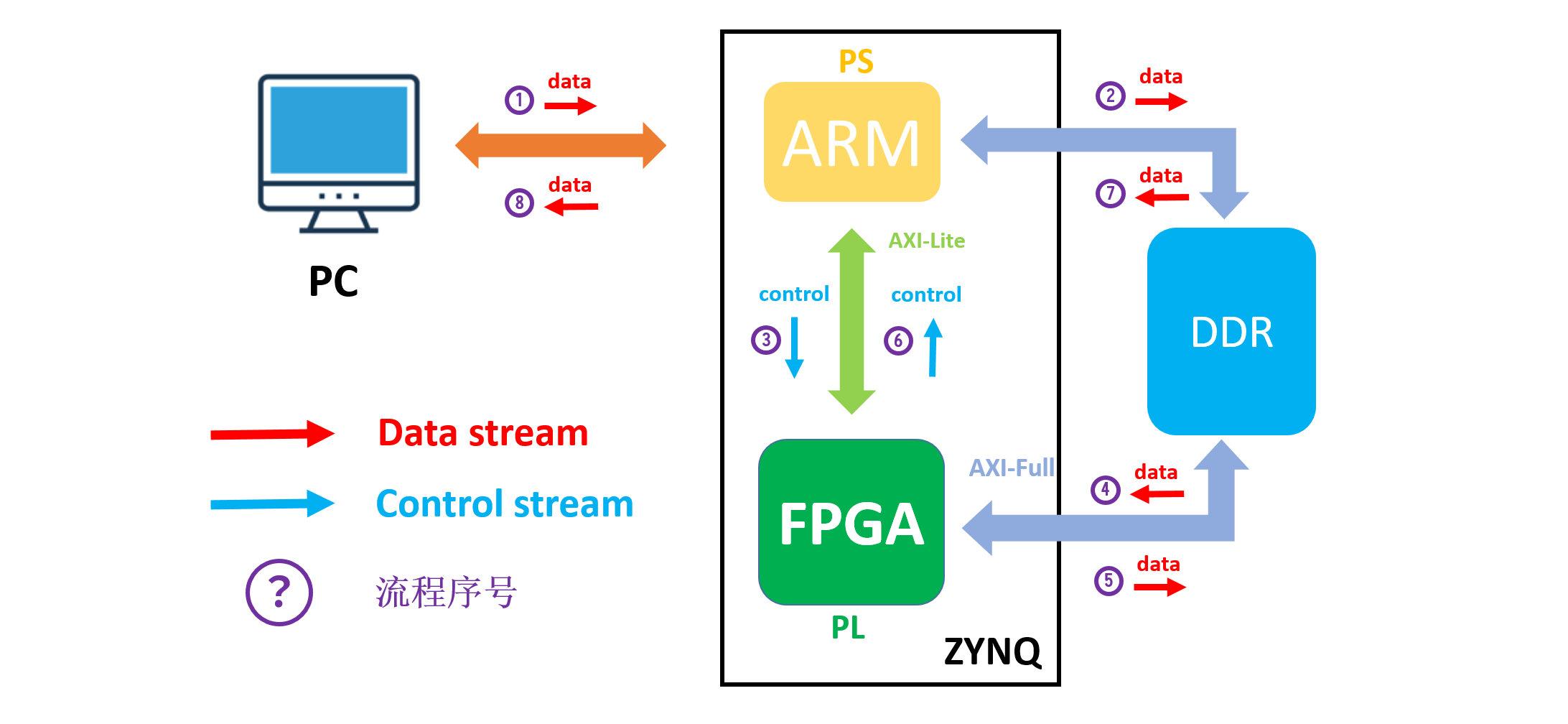

CNN 加速器的架构主要包括输入缓存，加速器ip以及输出缓存。FPGA 的数据读入主要利用 AXI-HP 接口，从 DDR 中来获取图片数据和参数数据，然后加速器计算完成后再将结果写回 DDR 中，其加速器的架构图如图3所示：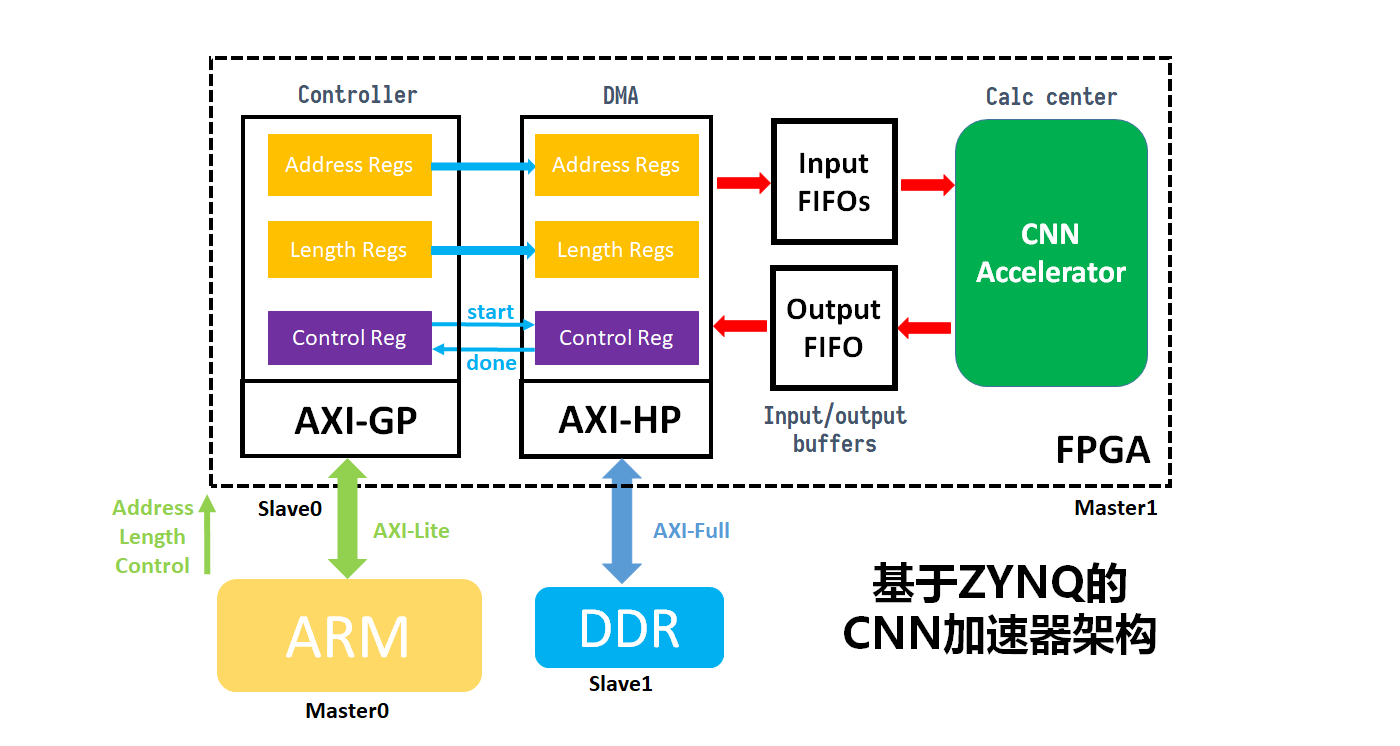

卷积核计算电路的设计

首先，整个卷积计算电路单元模块化设计如图4所示。它包括数据缓存模块、卷积计算模块以及数据剔除模块。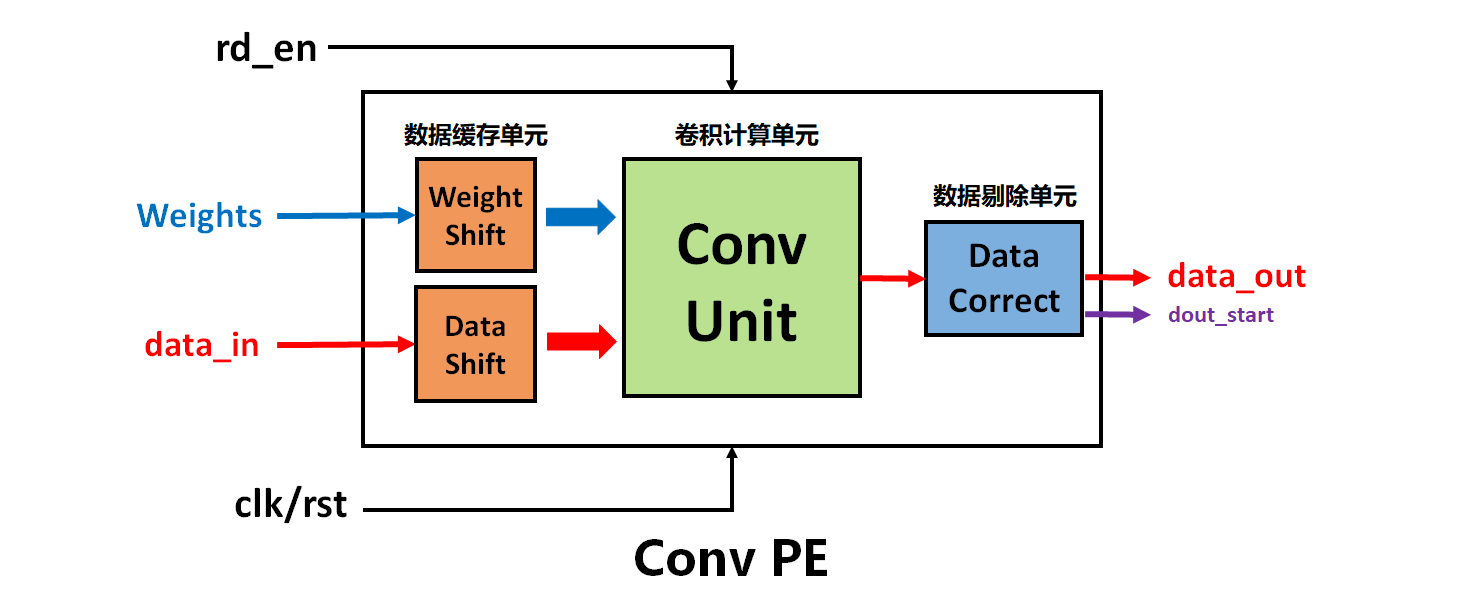

数据缓存模块

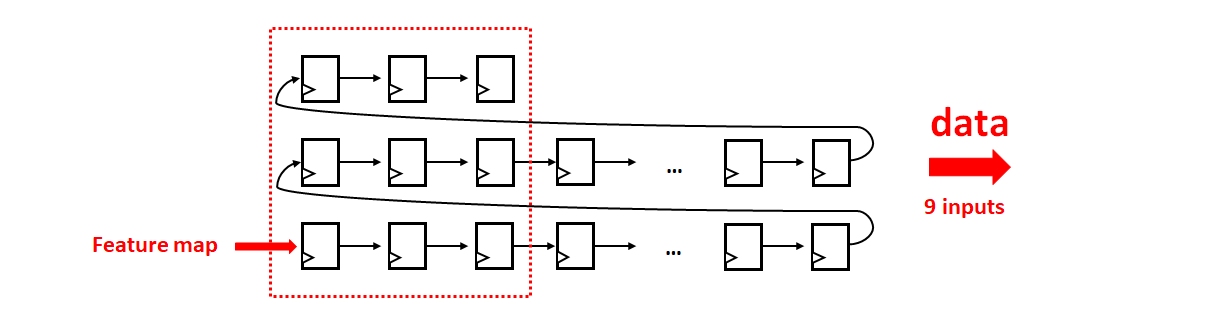
由于输入图像是以数据流形式输入，而卷积计算通过滑窗对卷积核内的数据进行乘累加操作，因此我用三个移位寄存器组将输入数据流分成三行，对应于 3x3 的卷积核。同理，权重数据流也是类似操作，如图5所示：

卷积计算单元

卷积计算在硬件电路实现时可以有效利用其并行性，以 3x3 的卷积核为例，常见的硬件实现方案都是使用乘法矩阵和加法树进行计算，以下是两种常见的硬件实现方案：

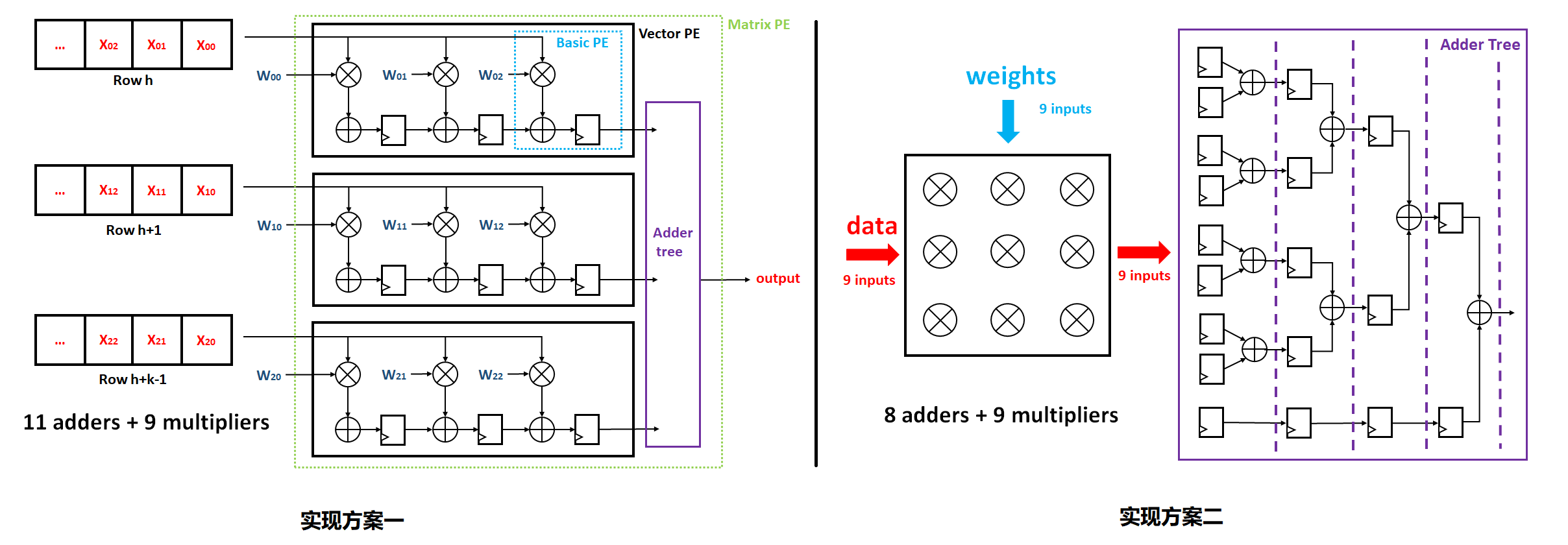
根据上述两种方案的设计结构，我采用了使用加法器更少的方案二，这样可以有效地节省 FPGA 的硬件资源，并且该方案的思路可以同时应用于池化层的设计。

数据剔除模块

另外，在设计过程中发现，在卷积计算过程中，计算完成一行后会从下一行的第一列重新计算，但实际输入数据以数据流的形式输入，依次输入前后数据是连续的，数据流进行中会产生前一行的末尾数据与后一行的开头数据进行卷积的错误结果，因此需要将这些数据进行剔除。根据仿真波形的观察，错误数据的出现是有规律的，因此利用一个FIFO作为缓存，当数据到来的同时产生一个脉冲控制信号，控制FIFO的写入，通过设置剔除信号的占空比来剔除掉错误数据，将正确的数据写入FIFO中，然后在保证数据完整正确的情况下再从FIFO中读出。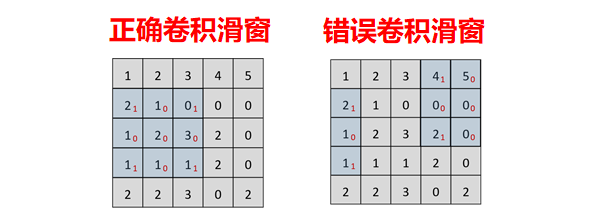

为了尽可能减少数据剔除中FIFO缓存的等待时间，假设输入图像大小为 ${n}\times{n}$, 卷积核的大小为 ${3}\times{3}$, 读入 $k$ 个数据后自动读出，则正确的输出数据个数为
$$
l = (n-2)^2\tag{1}
$$
又 FIFO 读入速度为
$$
v1 = \frac{n-2}{n}\tag{2}
$$
FIFO 读出速度为
$$
v2 = 1\tag{3}
$$
故为了保证数据不丢失, 则
$$
\frac{k}{v2-v1} = \frac{l}{v2}\tag{4}
$$
因此
$$
k = \frac{2(n-2)^2}{n}(向上取整)\tag{5}
$$
其中 $k$ 值在 FIFO ip核的 prog full 阈值中设定。根据 prog full 信号,读入 $k$ 个数据后自动读出,这样既保证数据的不丢失，又可以减少缓存带来的等待时间。

卷积计算电路的仿真

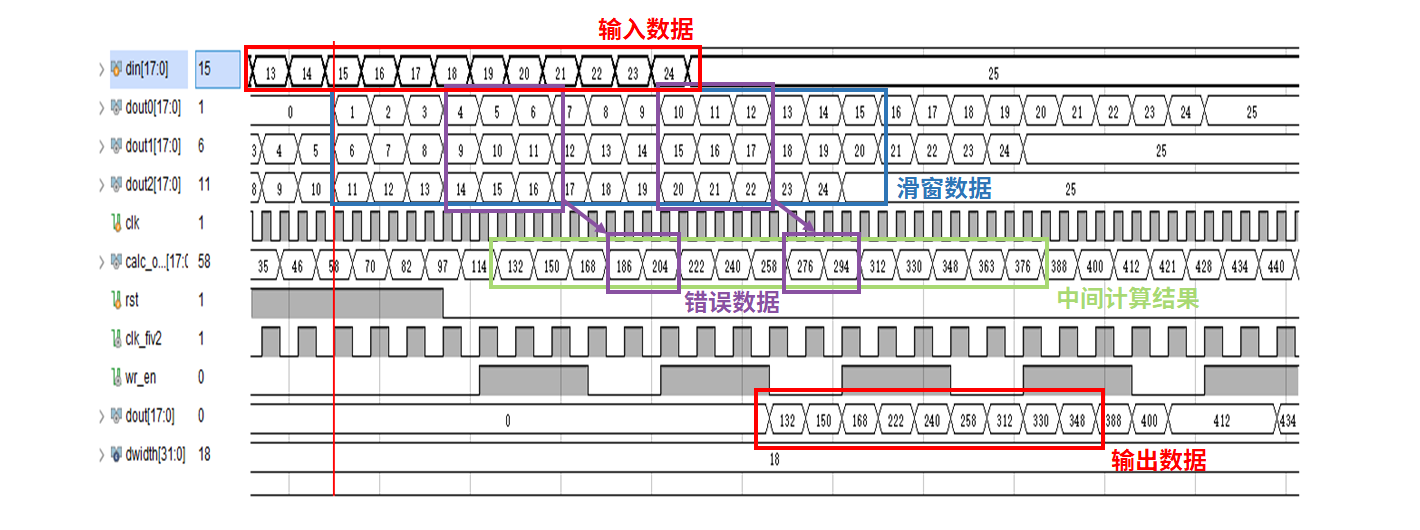
卷积计算电路仿真波形图如图8所示，其中，输入数据流为$\left[\begin{matrix}1 & 2 & \cdots & 5\\6 & 7 & \cdots & 10\\\vdots & \vdots & \ddots &\vdots\\21 & 22 & \cdots & 25 \end{matrix}\right]$, 权值矩阵为$\left[\begin{matrix}1 & 2 & 3\\1 & 2 & 3\\1 & 2 & 3\end{matrix}\right]$。

总结和计划

3月主要完成了CNN网络模型的训练和基本卷积电路计算单元的设计，并且完成了数据定点化的工作和卷积计算电路的仿真验证工作,原预期计划内容已基本完成。下一阶段打算完成池化层、全连接层等电路的设计和验证工作，完成整个卷积网络加速器的架构设计，并搭建好加速器外围数据写入和读出的硬件电路，进行上板测试。

参考文献

• [1] Qiu, Jiantao, et al. “Going deeper with embedded fpga platform for convolutional neural network.” Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. 2016.
• [2] Ma, Yufei, et al. “Scalable and modularized RTL compilation of convolutional neural networks onto FPGA.” 2016 26th International Conference on Field Programmable Logic and Applications (FPL). IEEE, 2016.
• [3] Guo K, Zeng S, Yu J, et al. A survey of fpga-based neural network accelerator[J]. arXiv preprint arXiv:1712.08934, 2017.
• [4] Sankaradas, Murugan, et al. “A massively parallel coprocessor for convolutional neural networks.” 2009 20th IEEE International Conference on Application-specific Systems, Architectures and Processors. IEEE, 2009.
• [5] Zhai, Sheping, et al. “Design of Convolutional Neural Network Based on FPGA.” Journal of Physics: Conference Series. Vol. 1168. No. 6. IOP Publishing, 2019.
• [6] 秦华标,曹钦平.基于FPGA的卷积神经网络硬件加速器设计[J].电子与信息学报,2019,41(11):2599-2605.
• [7] 余子健. 基于FPGA的卷积神经网络加速器[D].浙江大学,2016.